Matrizen, Grundrechenarten
Eine m x n-Matrix A=(aij) ist ein rechteckiges Zahlenschema der Form
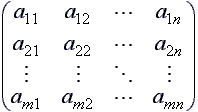
wobei die Koeffizienten aij (meist reelle oder komplexe) Zahlen sind. Die Zahlen m und n bezeichnen die Anzahl der Zeilen bzw. Spalten. Ein Vektor ist eigentlich nichts anderes als eine n x 1-Matrix.
Matrizen verhalten sich bezüglich der Addition und der Multiplikation mit einem Skalar genauso wie ein Vektor:
Matrizen-Multiplikation
Zausätzlich existiert für Matrizen ein Matrixprodukt, das nicht ganz so leicht zu berechnen ist: Zunächst einmal gilt es zu beachten, dass die Matrizen-Multiplikation in aller Regel nicht kommutativ ist (AB ist meist nicht gleich BA). Der erste Faktor muss zudem genau so viele Spalten besitzen, wie der zweite Faktor Zeilen. Eine 2×3-Matrix kann man mit einer 3×5-Matrix multiplizieren (das Ergebnis ist eine 2×5-Matrix), aber nicht umgekehrt!
Um nun die m x n-Matrix A mit der n x r-Matrix B zu multiplizieren, geht man wie folgt vor:
Um den Koeffizienten in der i-ten Zeile und der j-ten Spalte der Ergebnis-Matrix zu berechnen, multipliziert man
- den ersten Eintrag der i-ten Zeile von A mit dem ersten Eintrag der j-ten Spalte von B,
- den zweiten Eintrag der i-ten Zeile von A mit dem zweiten Eintrag der j-ten Spalte von B,
… - den letzten Eintrag der i-ten Zeile von A mit dem letzten Eintrag der j-ten Spalte von B
und addiert die Ergebnisse. Wenn Sie an das Skalarprodukt im 
denken, sollte Ihnen das Prinzip bereits bekannt vorkommen (das Skalarprodukt im ist im Grunde genommen das Matrixprodukt einer 1×3-Matrix und einer 3×1-Matrix). Die folgende Grafik soll das ganze verdeutlichen.
Für das Verständnis der hier vorgestellten Quantenspiele reicht es indes völlig aus, wenn Sie wissen, wie eine 2×2-Matrix mit einem zweidimensionalen Vektor multipliziert wird. Die Komplexität der Berechnung ist hier deutlich geringer:
Matrizen und lineare Abbildungen (in zwei Dimensionen)
Unter den Vektor-Abbildungen sind besonders die linearen Abbildungen von Interesse. Sie sind durch folgende Eigenschaft gekennzeichnet:
Anders ausgedrückt heißt das: Es ist egal, ob man erst addiert bzw. Skalar-multipliziert und anschließend die Abbildung f anwendet, oder umgekehrt, das Ergebnis ist stets dasselbe.
Um eine lineare Abbildung zu definieren, genügt es bereits, die Bilder der kanonischen Basisvektoren anzugeben:
Das Bild eines allgemeinen Vektors berechnet sich dann folgendermaßen:
Das heißt also: Es wird einfach die Matrix, deren Spalten aus den Bildern der Basisvektoren bestehen, mit dem Vektor multipliziert. Somit kann man mit einer einzigen Matrix eine komplette lineare Abbildung definieren. Die Matrix heißt deswegen die „darstellende Matrix“ der Abbildung (bezüglich der kanonischen Basis).
Matrizen in der Quantenmechanik (zweidimensionale Zustände)
Das besondere an quantenmechanischen Systemen ist, dass sie neben den klassisch messbaren Eigenzuständen 
und 
auch komplexere Zustände, sogenannte Superpositionen, annehmen können. Diese Zustände stellen Linearkombinationen 
der Eigenzustände dar. Die ohnehin bereits linear unabhängigen Eigenzustände bilden somit die Basis eines Vektorraums.
Da die Wellenfunktion eines Quantenzustands normiert sein muss, müssen auch die Linearkombinationen aus den Eigenzuständen normiert sein. Ein Vektorraum, der nur (komplexwertige) Vektoren vom Betrag eins besitzt, wird als Hilbertraum bezeichnet.
Den Manipulationen an quantenmechanischen Zuständen entsprechen lineare Abbildungen des Hilbertraums. Wegen der besonderen Struktur des Hilbertraums sind dabei nur bestimmte Arten von linearen Abbildungen möglich, die sogenannten unitären Abbildungen. Die genaue Definition einer unitären Abbildung ist recht kompliziert, für das Verständnis dieser Lektion aber nicht notwendig. Deswegen seien hier nur zwei wichtige Eigenschaften der darstellenden Matrix einer unitären Abbildung genannt:
- Die Matrix ist invertierbar, d.h. ihre Spaltenvektoren sind linear unabhängig.
- Der Betrag ihrer Determinante ist gleich eins.