9. Formalismus

Übersicht über den quantenmechanischen Formalismus

9.1 Zustände – 9.2 Operatoren – 9.3 Erwartungswerte – 9.4 Vertauschungsrelationen – 9.5 Selbstkontrolle – 9.6 Zusammenfassung

Diese Lektion soll als kurzer „Auffrischungskurs“ zum quantenmechanischen Formalismus dienen. Die theoretischen Elemente, die in den folgenden Kapiteln eingeführt werden, sollen in einen übergeordneten Zusammenhang gestellt werden. In einer kurzen Übersicht werden deshalb die wichtigsten Elemente des quantenmechanischen Formalismus zusammengestellt.

9.1 Zustände

In der klassischen Mechanik wird der Zustand eines Körpers durch die Angabe des Orts und der Geschwindigkeit zu einem bestimmten Zeitpunkt t festgelegt. Mit den Newtonschen Gesetzen kann man daraus auf die weitere Bewegung des Körpers schließen. Man kann aus den durch die anfängliche Präparation festgelegten Anfangsbedingungen seine Bahn errechnen.

In der Quantenmechanik ist das zentrale Objekt die Wellenfunktion $\psi(x)$ , die schon in Lektion 5 qualitativ eingeführt wurde. Kennt man die mathematische Form der Wellenfunktion, hat man die vollständige Information über das betreffende System. Man kann Wahrscheinlichkeitsverteilungen, Erwartungswerte und Streuungen für jede Observable berechnen.

Wie kann man Quantenobjekten eigentlich ansehen, durch welche Wellenfunktion sie beschrieben werden? Die Wellenfunktion ist keine Größe, die direkt messbar ist. Das sieht man schon daran, dass sie im Allgemeinen komplexwertig ist. Es kann also kein Messgerät geben, an dem man den Wert von „ $\psi(x,t)$ “ direkt ablesen kann.

Hier zeigt wieder einmal der Begriff der Präparation seine Nützlichkeit. Denn das Präparationsverfahren, dem ein Ensemble von Quantenobjekten unterworfen wurde, bestimmt seinen Zustand, d. h. seine Wellenfunktion.

Als Beispiel kommen wir auf die Elektronen zurück, die in der Elektronenstrahlröhre auf die Eigenschaft „kinetische Energie“ präpariert werden (Lektion 8). Ihnen wird die Wellenfunktion $\psi_{E_{kin}}$ zugeordnet, d. h. der Eigenzustand der kinetischen Energie, der den präparierten Wert der kinetischen Energie als Eigenwert besitzt.

Die Präparation bestimmt die Wellenfunktion eines Ensembles von Quantenobjekten.

Unter Präparation muss man dabei nicht immer einen künstlich im Labor erzeugten Prozess verstehen: Quantenobjekte können auch „spontan“ präpariert werden. Zum Beispiel sind angeregte Zustände von Atomen nicht sehr langlebig. Man kann also davon ausgehen, dass sich Atome im Grundzustand befinden, wenn man ausschließen kann, dass Anregungen durch Stöße, Licht o.ä. stattfinden. Der Grundzustand von Atomen wird insofern spontan präpariert.

Als Lösung der Schrödinger-Gleichung ist ein Zustand $\psi$ nur bis auf eine multiplikative Konstante festgelegt. Der Zustand $c \cdot \psi$ mit der (komplexen) Konstante $c$ ist ebenfalls eine Lösung der Schrödinger-Gleichung.

Üblicherweise lässt man die Konstante $c$ jedoch nicht offen, sondern normiert die Wellenfunktion. Man fordert:

$\int_V dV \psi^*(\vec{x}) \cdot \psi(\vec{x})=1$

Die Interpretation dieser Gleichung ist offensichtlich: $\psi^*(\vec{x}) \psi({\vec{x})$ ist die Aufenthaltswahrscheinlichkeitsdichte, das Elektron bei einer Messung im Volumenelement $\Delta V$ um den Ort Vektor $x$ herum zu finden. Die Normierung der Wellenfunktion wird so festgelegt, dass die Wahrscheinlichkeit, das Elektron bei einer Messung irgendwo im betrachteten Volumen zu finden, Eins wird.

9.2 Operatoren

Messgrößen (Observablen) werden in der Quantenmechanik durch Operatoren beschrieben. Einige Beispiele für Operatoren (kinetische Energie, Gesamtenergie) wurden schon in Lektion 8 diskutiert.

Die mathematische Form der gebräuchlichsten Operatoren lässt sich leicht durch die folgenden Regeln ermitteln:

Man drückt die entsprechende klassische Größe durch Ort und Impuls aus
(z. B.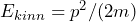 $E_{kinn}= p^2 / (2m)$ ).
Man ersetzt $p \rightarrow \frac{\hbar}{i} \frac{\partial}{\partial x}$ .
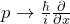Funktionen von 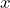$x$ bleiben unverändert.

Der Operator für die kinetische Energie wird dann:

$\hat{E}_{kin} = - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2}$

in Übereinstimmung mit dem Ergebnis aus Kapitel 8.

Andere Beispiele für Operatoren, die man auf diese Weise erhalten kann, sind:

Gesamtenergie:	$E_{ges}= \frac{p^2}{2m}+V(x) \rightarrow \hat{E}_{ges} = - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} +V(x)$
Drehimpulskomponente:	$L_z = x \cdot p_y - y \cdot p_x \rightarrow \hat{L}_z = \frac{\hbar}{i} \left( x \cdot \frac{ \partial}{\partial y} - y \cdot \frac{\partial}{\partial x} \right)$

Daneben gibt es auch Operatoren (wie z. B. den Spin-Operator), deren Form nicht auf diese einfache Weise erraten werden kann. Hier ist man auf Versuch und Irrtum angewiesen.

Den Operatoren fällt in der Quantenmechanik die Rolle zu, die in der Wellenfunktion enthaltene Information herauszuholen. Eine Möglichkeit, um mit Operatoren Information aus der Wellenfunktion zu extrahieren, wurde bereits besprochen: der Weg über die Eigenwertgleichung (Lekt. 8.6). Mit der Eigenwertgleichung für Operatoren lassen sich weiterhin die möglichen Messwerte theoretisch bestimmen.

Dem mathematischen Ausdruck einer Wellenfunktion sieht man es nicht auf Anhieb an, ob sie Elektronen mit der Eigenschaft „kinetische Energie“ oder „Drehimpuls“ beschreibt. Möchte man z. B. wissen, ob ein Ensemble von Elektronen, das durch die Wellenfunktion $\psi$ beschrieben wird, die Eigenschaft „kinetische Energie“ besitzt, wendet man den Operator der kinetischen Energie auf die Wellenfunktion an. Wird sie reproduziert, dann ist die Eigenwertgleichung $\hat{E}_{kin} \psi_{E_?} = E_{kin} \cdot \psi_{E_?}$ (!!!!!!) erfüllt. Die betreffenden Elektronen besitzen dann die Eigenschaft „kinetische Energie“. Man kann jedem Mitglied des Ensembles einen bestimmten Wert der kinetischen Energie zuordnen (der durch den Eigenwert gegeben ist).

In Lektion 8 wurde die Eigenwertgleichung als Maschine symbolisiert, mit der man entscheiden kann, ob einem Ensemble von Quantenobjekten die betreffende Eigenschaft zukommt und wenn dies der Fall ist, ihren Wert ablesen kann.

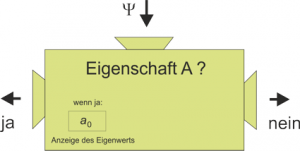
Bei einem quantenmechanischen Problem ist das Suchen von Eigenwerten und Eigenzuständen eine der Hauptaufgaben. Die stationäre Schrödinger-Gleichung ist die Eigenwertgleichung der Gesamtenergie, und der Grund warum man sie löst ist, dass man die Eigenwerte der Energie theoretisch vorhersagen möchte.

Eigenwerte sind deshalb wichtig, weil sie die möglichen Messwerte sind. Dies wurde schon im Zusammenhang mit dem Messpostulat in Lektion 6 diskutiert. Bei jeder Messung einer physikalischen Größe wird ein ganz bestimmter Wert gefunden, und zwar einer der Eigenwerte der gemessenen Größe.

Beispiele:

Beim Doppelspaltversuch mit Lampe in Kapitel 6 war die gemessene Größe der Ort, und jedes Elektron wurde an einem ganz bestimmten Ort hinter einem der beiden Spalte gefunden.
Löst man die Schrödinger-Gleichung für das Wasserstoffatom, erhält man ganz bestimmte Energie-Eigenwerte. Die Vorhersage der Quantenmechanik ist, dass bei einer Messung der Energie nur einer dieser Werte gefunden werden kann.

Misst man das Spektrum eines Wasserstoffatoms, führt man (wegen $E = h \cdot f$ ) eine Energiemessung durch. Die Vorhersage der Quantenmechanik bestätigt sich; es werden nur ganz bestimmte Energiewerte gefunden.

9.3 Erwartungswerte

Noch eine andere Art von Vorhersage wird mit Operatoren möglich. Man kann damit Erwartungswerte berechnen. Experimentell entspricht dem Erwartungswert der statistische Mittelwert sehr vieler Messwerte.

Die allgemeine Formel für den Erwartungswert einer physikalischen Größe lautet in der Quantenmechanik

$\langle A \rangle = \int dx \psi^*(x) \hat{A} \psi(x). \hspace{35pt} (1)$

Dabei ist $\hat{A}$ der zu der betreffenden physikalischen Größe gehörende Operator.

Betrachten wir ein Ensemble von Quantenobjekten, z. B. Elektronen in einem Elektronenstrahl. Die Elektronen werden durch die Wellenfunktion $\psi(x)$ beschrieben. Wenn man den Erwartungswert der kinetischen Energie berechnen möchte, muss man den Operator der kinetischen Energie

$\hat{E}_{kin} = - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2}$

in die Formel $(1)$ einsetzen und die Integration ausführen.

Was bedeutet der Wert, den man mit Formel $(1)$ errechnet hat? Wie kann man ihn mit experimentellen Daten in Verbindung bringen? Hier kommt wieder die statistische Deutung ins Spiel. Der Erwartungswert ist eine statistische Größe, die sich auf zahlreiche Messungen an verschiedenen Mitgliedern eines Ensembles bezieht.

Für das Beispiel der kinetischen Energie bedeutet das genauer:

1. Man benötigt: Ein Ensemble von identisch präparierten Elektronen, die durch die Wellenfunktion $\psi$ beschrieben werden.
2. Man führt Messungen der kinetischen Energie an vielen Elektronen dieses Ensembles durch.
3. Man bildet den Mittelwert der gemessenen kinetischen Energien. Er muss im Rahmen der Messgenauigkeit den gleichen Wert wie der mit Formel $(1)$ berechnete Erwartungswert besitzen.

9.4 Vertauschungsrelationen

Einige Operatoren sind nicht vertauschbar. Das bedeutet: Die Reihenfolge, in der sie auf eine Wellenfunktion angewendet werden, spielt eine Rolle. Bekanntestes Beispiel sind Ort und Impuls. Für sie gilt:

$\hat{p} \hat{x} \psi(x) \neq \hat{x} \hat{p} \psi (x).$

Wenn wir die explizite Form der Operatoren einsetzen, ergibt sich nämlich mit der Kettenregel:

${\begin{aligned} \hat{p} \hat{x} \psi(x) &\left = - i \hbar \frac{d}{dx} \left( x \psi(x) \right) \\ &\left = i \hbar \psi(x) - i \hbar x \frac{d}{dx} \psi(x) \\ &= i \hbar \psi(x) + \hat{x} \hat{p} \psi(x). \end{aligned$

Wir können also schreiben: $[ \hat{x}, \hat{p}] \psi(x) \equiv (\hat{x} \hat{p} -\hat{p} \hat{x}) \psi(x) = i \hbar \psi(x)$
oder $[ \hat{x}, \hat{p}] = i \hbar$

Die Größe $[\hat{A}, \hat{B}]$ nennt man den Kommutator der beiden Operatoren $\hat{A}$ und $\hat{B}$ .

Die mathematische Tatsache, dass zwei Operatoren nicht miteinander vertauschbar sind (ihr Kommutator von Null verschieden ist), wäre nicht weiter bemerkenswert, wenn nicht die Unbestimmtheitsrelation damit verbunden wäre.

Für zwei Operatoren, die nicht miteinander vertauschbar sind, gilt eine Unbestimmtheitsrelation mit allen Konsequenzen, die wir in Lektion 7 diskutiert haben. Man kann z. B. ein Ensemble von Quantenobjekten nicht gleichzeitig auf die beiden betreffenden Eigenschaften präparieren.

Für zwei physikalische Größen $A$ und $B$ (z. B. Ort und Impuls) mit der Vertauschungsrelation $[\hat{A}, \hat{B}] = i \hat{C}$

lautet die Unbestimmtheitsrelation:

$\Delta A \cdot \Delta B \geqslant \frac{1}{2} \left| \langle \hat{C} \rangle \right| \hspace{35pt} (2)$

Dabei sind $\Delta A$ und $\Delta B$ wie in Kapitel 7 als Streuungen definiert.

Wenn die beiden Operatoren vertauschbar sind, wird die rechte Seite zu Null. Gleichung $(2)$ reduziert sich dann zu der trivialen Aussage, dass ein Produkt zweier positiver Größen nicht negativ sein kann.

Für Ort und Impuls ist
$[ \hat{x}, \hat{p}] = i \hbar$ ,

so dass sich wieder die Relation
$\Delta x \cdot \Delta p \geqslant \frac{\hbar}{2}$ ergibt.

9.5 Selbstkontrolle

Wenn Sie dieses Kapitel durchgearbeitet haben, sollten Sie die folgenden Fragen beantworten können:

Weshalb wird die Wellenfunktion auf Eins normiert?
Welcher Zusammenhang besteht zwischen Messgrößen und Operatoren?
Durch welche Regeln kann man quantenmechanische Operatoren aus den entsprechenden klassischen Größen gewinnen?
Wenn für ein physikalisches System die Eigenwertgleichung für einen bestimmten Operator erfüllt ist: Was sagt dies für das betreffende System aus?
Wie kann man die möglichen Messwerte einer Observablen theoretisch bestimmen?
Wie berechnet man Erwartungswerte?
Was entspricht dem quantenmechanischen Erwartungswert im Experiment?
Was versteht man unter Vertauschungsrelationen?
Welche physikalische Konsequenz hat es, wenn zwei Operatoren nicht miteinander vertauschbar sind?

9.6 Zusammenfassung von Lektion 9:
Übersicht über den quantenmechanischen Formalismus

Als Zusammenfassung finden Sie hier die Antworten auf die Fragen aus der Selbstkontrolle.

Weshalb wird die Wellenfunktion auf Eins normiert?
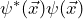$\psi^*(\vec{x}) \psi(\vec{x})$ ist die Aufenthaltswahrscheinlichkeitsdichte der Elektronen. Die Wellenfunktion wird auf Eins normiert, damit die Wahrscheinlichkeit, ein Elektron bei einer Messung irgendwo im betrachteten Volumen zu finden, Eins wird:

$\int_V dV \psi^*(\vec{x}) \cdot \psi(\vec{x}) = 1$
Welcher Zusammenhang besteht zwischen Messgrößen und Operatoren?
Jeder Messgröße wird in der Quantenmechanik ein Operator zugeordnet. Mit den in diesem Kapitel vorgestellten Regeln kann man theoretische Vorhersagen über die jeweilige Messgröße treffen (z. B. Erwartungwerte oder die möglichen Messwerte berechnen).
Durch welche Regeln kann man quantenmechanische Operatoren aus den entsprechenden klassischen Größen gewinnen?
Man ersetzt im klassischen Ausdruck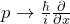 $p \rightarrow \frac{\hbar}{i} \frac{\partial}{\partial x}$ ; Funktionen von x bleiben unverändert.
Wenn für ein physikalisches System die Eigenwertgleichung für einen bestimmten Operator erfüllt ist: Was sagt dies für das betreffende System aus?
Wenn z. B. die Eigenwertgleichung für die kinetische Energie erfüllt ist, bedeutet das, dass die betreffenden Elektronen die Eigenschaft „kinetische Energie“ tatsächlich besitzen. Bei jeder Messung der kinetischen Energie wird ein ganz bestimmter Wert gefunden.
Wie kann man die möglichen Messwerte einer Observablen theoretisch bestimmen?
Die möglichen Messwerte einer Observablen sind ihre Eigenwerte. Diese müssen also berechnet werden. Für Elektronen im Coulomb-Potential (H-Atom) z. B. gibt es ganz bestimmte Eigenwerte der Gesamtenergie. Nur diese Werte werden bei Energiemessungen gefunden, was sich z. B. im Auftreten von Linienspektren bemerkbar macht.
Wie berechnet man Erwartungswerte?
Die Formel lautet: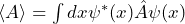 $\langle A \rangle = \int dx \psi^*(x) \hat{A} \psi(x)$ .
Was entspricht dem quantenmechanischen Erwartungswert im Experiment?
Im Experiment entspricht dem Erwartungswert der statistische Mittelwert sehr vieler Messwerte der betrachteten Größe, die an identisch präparierten Quantenobjekten gewonnen wurden.
Was versteht man unter Vertauschungsrelationen?
Bei vielen Operatoren spielt die Reihenfolge eine Rolle, in der sie auf eine Wellenfunktion angewendet werden. Die Vertauschungsrelationen bringen dies formal zum Ausdruck.
Welche physikalische Konsequenz hat es, wenn zwei Operatoren nicht miteinander vertauschbar sind?
Für zwei Operatoren, die nicht miteinander vertauschbar sind, gilt die Unbestimmtheitsrelation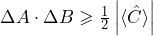 $\Delta A \cdot \Delta B \geqslant \frac{1}{2} \left| \langle \hat{C} \rangle \right|$ , wobei $\left[ \hat{A}, \hat{B} \right] = i \hat{C}$ .