11. Der Tunneleffekt

11.1 Der Tunneleffekt – 11.2 Der Tunneleffekt in Natur und Technik – 11.3 Simulationsprogramme von Zollman – 11.4 Der Tunneleffekt in der Schule
11.5 Selbstkontrolle – 11.6 Zusammenfassung

„In der Quantenwelt ist es möglich, sich durch eine energetisch verbotene Zone schnell hindurchzumogeln.“ (Richard Feynman)

In diesem Kapitel wird der quantentheoretische Hintergrund dieses Zitats behandelt. Durch den Nobelpreis an Binnig und Rohrer im Jahr 1986 steht das Rastertunnelmikroskop im Zentrum der Anwendungen des Tunneleffekts.

Dieses Kapitel beinhaltet die Grundlagen, sowie allgemeine Information zum Tunneleffekt, aber es werden auch Vorschläge gegeben, wie in der Schule der Tunneleffekt besprochen werden kann.

11.1 Der Tunneleffekt

In Abschnitt 10.1 wurde der Potentialtopf behandelt, bei dem sich die Elektronen in gebundenen Zuständen befinden. Die Potentialbarriere geht aus dem Potentialtopf durch Spiegelung an der Horizontalen hervor (siehe Abb. 11.1). Die Potentialbarriere liefert allerdings ein gänzlich anderes Verhalten der Quantenobjekten als im Fall des Potentialtopfs. Es fehlen z.B. die gebundenen Zustände mit quantisierten Energieniveaus.

Abb.11.1: Potentialverlauf V_{(x)} und Gesamtenergie E \le V_0

Klassisch gesehen stellt für jedes Teilchen die Barriere ein Hindernis dar, das nicht überwunden werden kann, wenn die Gesamtenergie E des Teilchens kleiner als die Höhe V_0 der Barriere ist. In der Quantenmechanik ist das anders:

Eine von links einlaufende Welle wird teilweise reflektiert. Der restliche Teil geht aber durch die Barriere hindurch in das Gebiet III hinein. Dies geschieht, obwohl das Gebiet II aus energetischer Sicht für das Quantenobjekt verboten ist. Genauere Details bringt die Lösung der Schrödingergleichung mit sich:

Die Schrödingergleichung für die Potentialbarriere und ihre Lösung

Die Schrödingergleichung

    \[ \left( \hat{E}_{kin} + V_{(x)} \right) \psi_{(x)} = E \cdot \psi_{(x)} \]

lautet in den Gebieten I, II und III:

Gebiet I Gebiet II  Gebiet III
\displaystyle {-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi = E \cdot \psi} \displaystyle {- \left( \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V_0 \right) \psi = E \cdot \psi} \displaystyle {- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi = E \cdot \psi}
 umgeformt:
\displaystyle {\frac{d^2}{dx^2} \psi = -\frac{2mE}{\hbar^2} \cdot \psi}		  umgeformt:
\displaystyle {\frac{d^2}{dx^2} \psi = - \frac{2m(E-V_o)}{\hbar^2} \cdot \psi}		  umgeformt:
\displaystyle {\frac{d^2}{dx^2} \psi = - \frac{2mE}{\hbar^2} \cdot \psi}

Jede der Gleichungen besitzt jeweils zwei unabhängige Lösungsfunktionen. Um eine Lösung für das gesamte Gebiet zu erhalten, müssen die Lösungsteile geeignet zusammengesetzt werden, so dass die Übergänge stetig und stetig differenzierbar sind. Eine der möglichen Gesamtlösungen hat die folgende Form:

\psi_{(x)} = \left\lbrace \begin{array}{ccc} - \frac{k_2}{k_1}sin(k_1x) + cos(k_1x) \hspace{158pt} falls \: x \le 0 \\ exp(-k_2x) \hspace{200pt} falls \: 0 < x < a \\ exp(-k_2a) \cdot \left( - \frac{k_2}{k_1}sin(k_1(x-a)) + cos(k_1(x-a)) \right) \hspace{28pt} falls \: a \le x \end{array}

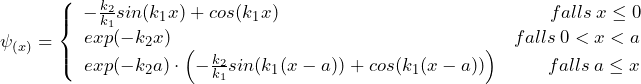
mit

    \[ k_1 = \frac{1}{\hbar} \sqrt{2mE} \hspace{15pt} und \hspace{15pt} k_2 = \frac{1}{\hbar} \sqrt{2m(E-V_0)} \]

Hier ist für das Gebiet II ausschließlich die exponentiell abfallende Teillösung verwendet worden. In diesem Fall ist die Intensität im Gebiet III nur ein Bruchteil von der Intensität im Gebiet I. In guter Näherung kann diese geringe Intensität in Gebiet III als durchtunnelter Anteil der Hauptwelle von Gebiet I betrachtet werden.

Warum ist dies nur eine Näherung?

Zur Bestimmung des Transmissionsgrades T werden die Intensitäten (Absolutquadrat der Wellenfunktion) der entsprechenden Gebiete bestimmt und ins Verhältnis gesetzt. Für die oben angegebene Wellenfunktion erhält man:

    \[ \displaystyle{ T = e^{- \sqrt{2m(E-V_0)} \frac{2a}{\hbar}}} \]

Der Transmissionsgrad T ist ein Maß dafür, wie gut die Barriere durchtunnelt werden kann: Je höher die Barriere im Vergleich zur Gesamtenergie ist, desto gringer ist die Wahrscheinlichkeit, dass die Barriere durchtunnelt wird.

11.2 Der Tunneleffekt in Natur und Technik

Dieser Abschnitt gibt einen kleinen Überblick über die Anwendungen des Tunneleffekts:

Feldelektronenmikroskop

Quelle: Das Quantenuniversum, Tony Hey und Patrick Walter, S. 89ff

Die Grundlage für diese Anwendung ist die Vorstellung, dass sich Elektronen in einem Metall bewegen können, näherungsweise wie im Inneren eines Potentialtopfs. Die Begrenzungsflächen des Metalls entsprechen den Wänden des Potentialtopfs, der von den Elektronen ohne Energiezufuhr nicht verlassen werden kann (vgl. Photoeffekt).

Abb.11.2 Potentialmodell eines Metalls

Wird das Metall (z.B. ein Draht oder eine kleine Kugel) stark negativ gegenüber der Umgebung aufgeladen, so ändert sich die Form des Potentials, siehe Abb. 11.3:

Abb. 11.3 Potentialmodell eines Metalls mit äußerem Feld

Die Barriere dieser Potentialform kann im Vakuum von den Elektronen mit einer gewissen Wahrscheinlichkeit durchtunnelt werden. Um beobachtbare Effekte zu erzielen sind allerdings dazu sehr hohe Feldstärken notwendig,. Deshalb eignen sich vor allem sehr dünne Metallspitzen. Schon 1928 konnte ein solcher „Feldemissionsprozess“ experimentell nachgewiesen worden.

Diesen Effekt nutzt man speziell beim Feldelektronenmikroskop. Elektronen, die die Potentialbarriere durchtunnelt haben, werden in dem äußeren elektrischen Feld (elektrische Feldstärke von ca. 109\frac{V}{m}) nahezu geradlinig beschleunigt. Umgibt man die Nadel mit einem phosphoreszierenden Schirm, erhält man ein stark vergrößertes Bild der Nadelspitze, das sich aus den Leuchtpunkten der aufprallenden Elektronen zusammensetzt. Da an den Ecken die Elektronen am leichtesten herausgelöst werden, werden diese Bereiche am hellsten abgebildet.

Beugungsphänomene der leichten Elektronen verhindern allerdings, dass einzelne Atome aufgelöst werden können. Dies erreicht man erst, wenn man für die Abbildung statt der Elektronen Ionen, speziell Heliumionen, verwendet. Dazu wird die Metallspitze positiv aufgeladen und von einem verdünnten Heliumgas umgeben. Die nahen Heliumatome geben Elektronen an die Spitze ab. Die restlichen positiven Ionen werden anschließend im elektrischen Feld beschleunigt. Diese Variante nennt man Feldionenmikroskop.

Die Vergrößerung der beiden Feldmikroskope liegt bei vielen Millionen bis einige Milliarden. Während beim Feldelektronenmikroskop Strukturen nur verschmiert abgebildete werden können, ist eine atomare Auflösung beim Feldionenmikroskop möglich.

          
Wolframnadel aufgenommen mit einem
a) Feldelektronenmikroskop                                         b) Feldionenmikroskop

Abbildungen aus „Das Quantenuniversum“
von T. Hey und P. Walters, S. 91
Rastertunnelmikroskop

Quelle: weitgehend nach Kuhn Physik 2, S.325 (1. Auflage 2000)

Zwischen zwei Leitern, die sich nahe beieinander befinden, aber keinen Kontakt miteinander haben, wird eine Spannung angelegt. Im Ultrahochvakuum können dann Elektronen durch die zwischen den Leitern bestehende Potentialbarriere tunneln. Es fließt ein Tunnelstrom, dessen Größe exponentiell mit der Breite der Potentialbarriere abfällt. Diese Abhängigkeit des Tunnelstroms ermöglicht die Konstruktion eines neuartigen Mikroskops, das alle bisher bekannten Mikroskope im Auflösungsvermögen um Größenordnungen übertrifft. Mit diesem Rastertunnelmikroskop, für dessen Erfindung G.Binning und H. Rohrer 1986 den Physiknobelpreis erhielten, kann man atomare Strukturen direkt sichtbar machen.

Abb. 11.4: Prinzipieller Aufbau des Rastertunnelmikroskops

Abb. 11.5: Das „kleinste Loch der Welt“: Aufnahme mit dem Rastertunnelmikroskop einer MoS2-Oberfläche, in der ein einzelnes Atom fehlt (Quelle: W.Heckl, LMU München)

Dazu rastert eine feine Nadel die Oberfläche des zu untersuchenden Objekts ab. Die Höhe der Nadel über der Oberfläche lässt sich sehr genau regulieren. Sie wird so eingestellt, dass zwischen der Nadelspitze und der Oberfläche ein nachweisbarer Tunnelstrom fließt. Beim Abrastern wird die Höhe der Nadel laufend so nachgeregelt, dass der Tunnelstrom einen konstanten Wert behält. Dies bewirkt, dass die Nadel immer ungefähr im gleichen Abstand zur Oberfläche bleibt. (Lokale Ladungsverschiebungen sowie Gitterdefekte können eine falsche Topologie vortäuschen.) Indem man die Nadelhöhe für jeden Punkt aufzeichnet, gewinnt man ein Höhenprofil der Oberfläche. Die Methode ist so empfindlich, dass man damit einzelne Atome in der Oberfläche ausmachen kann.

Der α-Zerfall

Quelle: Kuhn Physik 2, S. 368 (1. Auflage 2000)

Es stellt sich die Frage: Wieso kann ein α-Teilchen überhaupt den Kern verlassen, wenn seine Energie zur Überwindung des Potentialwalls nicht ausreicht? – Wenn Atome zerfallen, wieso dann nicht alle gleichzeitig?

Die Kernbausteine (Nukleonen) erfahren im Atomkern verschiede Kräfte, die zu einem Potential von ungefähr folgender Form führen:

Abb. 11.6: Klassisches Teilchen im Potentialtopf

Abb. 11.7: Quantenmechanisches Teilchen im Potentialtopf
Der Tunneleffekt erklärt den α-Zerfall

Alle Nukleonen werden durch eine kurzreichweitige Kernkraft angezogen. Dies führt zur Potentialmulde (in der Mitte). Die Protonen stoßen sich allerdings auch elektrostatisch ab. Da diese Kraft mit dem Abstand zwar schwächer wird, aber nicht gänzlich verschwindet, entsteht dieses Potential, das einem Vulkankegel gleicht.

Es gibt Sorten von Atomkernen, bei denen die Energie einzelner Nukleonen in der Mulde so hoch ist, dass die einzelnen Nukleonen auch außerhalb des Atomkerns existieren könnten. Der direkte Weg ist allerdings durch die Potentialbarriere versperrt. Als Quantenobjekte können die energiereicheren Nukleonen durch die Barriere hindurchtunneln. Einzelne Protonen können so vom Atomkern abdampfen.

Sehr viel häufiger als die Emission von einzelnen Nukleonen beobachtet man den alpha-Zerfall, also die Emission eines Helium-Atomkerns. Der Grund dafür liegt in der hohen Bindungsenergie der Nukleonen im alpha-Teilchen. Während häufig die Energie eines Nukleons im Atomkern nicht für den freien Zustand ausreicht, kann die Energie hoch genug sein, dass ein Verband von vier Nukleonen als alpha-Teilchen frei existieren kann. In diesem Fall kann ein alpha-Teilchen aus dem Atomkern heraustunneln, aber nicht ein einzelnes Nukleon. Wie gut die Wellenfunktionen der Nukleonen bzw. alpha-Teilchen die Barriere durchdringen können, wird durch die Potentialhöhe und Potentialbreite bestimmt. Die Intensität außerhalb des Atomkerns ist bei radioaktiven Kernen zwar klein, aber größer als null. Diese Intensität ist auch ein Maß dafür, wie leicht bzw. schnell Kerne dieser Sorte zerfallen.

Sonnenschein mit Hilfe des Tunneleffekts

Wie allgemein bekannt ist, erhält die Sonne ihre Energie durch Kernfusion. Dabei verschmelzen insgesamt vier Protonen zu einem Heliumkern und einigen leichteren Reaktionsprodukten. Da die für die Fusion wichtige Kernkraft nur eine sehr geringe Reichweite besitzt, müssen sich die geladenen Ionen sehr stark annähern, um zu verschmelzen. Sie benötigen deshalb eine ausreichende kinetische Energie, um die elektrostatische Abstoßung zu überwinden. In diesem Abschnitt wird durch eine Abschätzung gezeigt, dass die Ionen bei der Innentemperatur der Sonnen die notwendige kinetische Energie nicht besitzen können und deshalb andere Mechanismen (der Tunneleffekt) zum Tragen kommen müssen, damit die Sonne auf die beobachtete Weise funktioniert.

Abschätzung der Mindestenergie

Exemplarisch wird ein elementarer Fusionsprozess betrachtet. Zwei Protonen verschmelzen zu einem Deuterium und einigen leichteren Reaktionsprodukten:

    \[ ^1_1H+^1_1H \rightarrow ^2_1H +^0_1e +^0_0v \]

Damit die Protonen durch die Kernkraft angezogen werden, müssen sich die Protonen auf die Reichweite der starken Wechselwirkung annähern. Der notwendige Abstand beträgt ca. 1fm = 10^{-15}m; die Protonen müssen sich also fast berühren. Dafür wird eine kin. Energie von ca. 1 MeV benötigt (Um eine Annäherung auf exakt 1 fm zu ermöglichen, ist eine kin. Energie vom Betrag

    \[ E_{kin}= \frac{1}{4 \pi \epsilon_0} \cdot \frac{e^2}{1,0 fm} \]

von 1,4 MeV notwendig.)

Temperatur und Mindestenergie

Für die Temperaturabschätzung kann das Plasma im Sonneninneren als ideales Gas angesehen werden, bei dem die mittlere kinetische Energie gegeben ist durch:

    \[ \bar{E}_{kin}= \frac{3}{2} kT \]

Die abgeschätzte Mindestenergie von 1 MeV entspricht dann einer Temperatur von knapp 8 \cdot 10^9K. Die Innentemperatur der Sonne von ca. 15 Millionen Grad liegt um den Faktor 500, also ca. 3 Größenordnungen niedriger. Diese Diskrepanz kann nicht durch Fehler bei der Abschätzung erklärt werden.

Nachdem in einem Gas nicht alle Teilchen dieselbe Energie besitzen, könnte es jedoch sein, dass wenigstens ein kleinerer Teil der Ionen im Rahmen der Maxwell-Boltzmann-Verteilung diese kritischen Energie erreicht. Die Häufigkeitsverteilung fällt im interessanten Bereich allerdings exponentiell sehr schnell ab, so dass praktisch kein Teilchen in der Sonne die notwendige Energie besitzt. (Zwischen maximal besetzter Energie und der oben berechnete Mindestenergie liegen in der Antreffwahrscheinlichkeit mehr als 100 Größenordnungen. Bei ca. 10^57<span style="font-size: 13.3333px;"> Protonen besitzt die Sonne mit einer Wahrscheinlichkeit von weniger als 10^-43 ein geeignet energiereiches Proton.)

Die Sonne ist also zu kalt, um nach klassischer Theorie ihre Energie aus der Kernfusion beziehen zu können.

Der Tunneleffekt macht es möglich

Schon bei geringer Annäherung von zwei Protonen kann eine Fusion mit Hilfe des Tunneleffekts stattfinden: Die restliche Coulomb-Barriere kann quantenmechanisch überwunden werden. Die Tunnelrate ist umso größer, je näher sich die Protonen kommen. Allerdings sind ausreichende Annäherungen – wie oben abgeschätzt – sehr selten. Die Berücksichtigung der Geschwindigkeitsverteilung und der Tunnelwahrscheinlichkeit führt dazu, dass zwei Protonen von ungefähr 5 keV bei unserer Sonne am häufigsten zur Fusion beitragen (Gamov-Peak). Für die Verschmelzung von 2 He_3-Kernen zu einem He_4-Kern und zwei Protonen liegt das Maximum bei 21 keV.

Wie häufig bzw. selten sind nun Fusionsprozesse bei bestimmten Energien?

Um dies abschätzen zu können, wird hier der Transmissionsgrad (Tunnelwahrscheinlichkeit für ein Annäherungsereignis) für den Fall berechnet, dass sich zwei Protonen zentral bis auf einen Abstand x annähern. Das Potential U_{(r)} ist das Coulombpotential und die kinetische Energie ist U_{(x)}. Es wird hier angenommen, dass die Kernkraft unterhalb eines Abstands von x_0=1 fm wirkt und gegenüber der elektrischen Kraft dominiert.

    \[ T \approx exp \left( - \frac{2}{ \hbar} \int_{x_0}^x \sqrt{2m(U_{(r)}-U_{(x)})}dr \right) \]

In der folgenden Tabelle sind für einige Minimalabstände die zugehörigen Energien wie auch die Transmissionsgrade angegeben:

Abstand in 10-12 m     Energie in keV     Tunnelwahrscheinlichkeit  Bemerkung
 0,2  14  9 · 10-7
 0,5  5,8  1,6 · 10-10  ca. Energie mit max. Fusionsrate
 1,0  2,9  9 · 10-15  ca. häufigste Teilchenenergie
 2,0  1,4  9 · 10-21

Die Tunnelwahrscheinlichkeit hängt also sehr sensibel von dem erreichten, minimalen Abstand ab. Schon eine Verdopplung des Abstands entsprichte einer um viele Größenordnungen kleinere Tunnelwahrscheinlichkeit.

Die Tabellenwerte sind für zentrale Stöße abgeschätzt worden. Im realen Fall kommen aber zentrale Stöße so gut wie nie vor. Deshalb ist bei einer bestimmten Teilchenergie der minimale Abstand größer und die Fusionswahrscheinlichkeit noch bedeutend niedriger. Dennoch liefert der Tunneleffekt den entscheidenden Beitrag dazu, dass der Fusionsreaktor Sonne läuft.

11.3 Simulationsprogramme von Zollman

In Abschnitt 10.4 wurde bereits ein Teil der Simulationsprogramme aus „Visual Quantum Mechanics“ der Kansas State Universitiy beschrieben. Hier werden kurz die entsprechenden Simulationen zum Tunnneleffekt vorgestellt:

Quantum Tunneling

Die Simulation gibt die in Abschnitt 11.1 beschrieben Situation eines Teilchens wieder, das durch eine Barriere tunnelt. Die stationäre Lösung der Schrödingergleichung wird als Näherung für den Transportprozess einer Welle durch die Barriere verwendet. Zwei Phänomene lassen sich in dieser Simulation besonders gut untersuchen:

  1. Das Verhältnis der Intensitäten vor und hinter der Barriere („Probability Density“),
  2. die Abhängigkeit des Transmissionsgrads von der Teilchenenergie bzw. Teilchenart („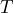T vs. E„).

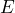Je nach Wunsch kann auch der reale bzw. imaginäre Teil der Wellenfunktion oder die Wahrscheinlichkeitsdichte angezeigt werden. Der Benutzer kann die Form sowie die Höhe der Potentialbarriere unter „Barrier Parameters“ selbst auswählen. Die Art der Teilchen (Elektron, Pion, …) wird mit „Particle Parameters“ bestimmt. Zusätzlich kann unter „Planck’s Constant“ der Wert von h verändert werden.

http://phys.educ.ksu.edu/vqm/html/qtunneling.html

Quantum Motion

Hier wird in einem Film die zeitliche Entwicklung einer Welle gezeigt, die an einem skalierbaren Potential gestreut wird. Es können auch hier zwei Potentiale hintereinandergeschachtelt werden.

https://perg.phys.ksu.edu/vqmorig/programs/java/qumotion/quantum_motion.html

11.4 Der Tunneleffekt in der Schule

Analogien zum Tunneleffekt

Bei diesen Ausführungen beziehen wir die Information aus: „Das Quantenuniversum“, Hey & Walters, S.85ff

Der Tunneleffekt mit Wellen:

Man kann den Tunneleffekt anhand der Totalreflexion des Lichtes demonstrieren. Auch hinter der totalreflektierenden Fläche tritt eine Lichtquelle auf, deren Amplitude mit dem Abstand von der Fläche exponentiell abnimmt. Wird ein zweites Prisma parallel zu der totalreflektierenden Glasfläche des ersten herangeschoben. Ist der Abstand so, dass die „abklingende Welle“ bis an das zweite Prisma heranreicht, bemerken wir einen Lichtstrahl im zweiten Prisma. Je näher die Prismen beieinander stehen, desto mehr Licht wird durchgelasssen, da die Amplitude in der verbotenen Luftschicht entsprechend weniger Zeit hat um abzuklingen. Man bezeichnet dieses Phänomen oft auch als „verhinderte Totalreflexion“. Dieses Phänomen ist nichts anderes als der quantenmechanische Tunneleffekt mit de Broglies Materiewellen. In der Optik wird dieser Effekt als Strahlteiler genutzt, um das Licht aufzusplitten.

Abb. 11.8: Tunneleffekt bei Totalreflexion

Das Experiment mit Licht ist in der Schule schwierig durchzuführen. Mit Mikrowellen und Paraffinprismen ist der Versuch sehr viel leichter zu realisieren.

Achterbahnmodell

Das Modell der Achterbahn ist eine sehr anschauliche Erklärung des Tunneleffekts. Ein Wagen startet aus der Ruhe im Punkt A. Wegen der Energieerhaltung kann er nicht höher als Punkt B hinauskommen. Doch aufgrund des Tunneleffekts besteht die Wahrscheinlichkeit den Wagen im Punkt C vorzufinden.

Hier finden Sie einen Versuchsaufbau zum Tunneleffekt.

 

11.5 Selbstkontrolle

Nach der Bearbeitung von Kapitel 11 sollten Sie folgende Fragen beantworten können:

  • Wie lautet die Schrödingergleichung für die drei Bereiche bei der Potentialbarriere?
  • Welcher Ansatz wird zur Lösung verwendet? Was gibt der Transmissionskoeffizient an und wovon hängt er ab?
  • Was versteht man unter dem Tunneleffekt?
  • Wie funktioniert
    1. das Feldelektronenmikroskop,
    2. das Rastertunnelmikroskop?
  • Wie lässt sich der α-Zerfall erklären?
  • Welche Möglichkeiten gibt es, den Tunneleffekt in der Schule zu veranschaulichen?

11.6 Zusammenfassung von Kapitel 11: Der Tunneleffekt

Der Tunneleffekt besagt, dass sich Teilchen durch energetisch verbotene Zonen hindurchbewegen können. Der Transmissionsgrad T lässt sich über die Lösung der stationären Schrödingergleichung abschätzen:

    \[ T = e^{- \sqrt{2m(E-V_0)} \frac{2a}{\hbar}} \]

Elektronen können durch starke elektrische Felder aus einem Metall in einen energetisch erlaubten Bereich des Feldes tunneln (Anwendung: Feldelektronenmikroskop).

Ebenso können Elektronen durch einen engen Spalt von einem Metall in ein anderes Metall tunneln (Anwendung: Rastertunnelmikroskop).

Beim α-Zerfall sind die tunnelnden Objekte α-Teilchen, die mit einer gewissen Wahrscheinlichkeit vom Kern emittiert werden.

Mit Hilfe der Totalreflexion von Licht oder Mikrowellen kann der Tunneleffekt veranschaulicht werden.
[

\bar{E}_{kin}= \frac{3}{2} kT

\]
Elektronen können durch starke elektrische Felder aus einem Metall in einen energetisch erlaubten Bereich des Feldes tunneln (Anwendung: Feldelektronenmikroskop).

Ebenso können Elektronen durch einen engen Spalt von einem Metall in ein anderes Metall tunneln (Anwendung: Rastertunnelmikroskop).

Beim α-Zerfall sind die tunnelnden Objekte α-Teilchen, die mit einer gewissen Wahrscheinlichkeit vom Kern emittiert werden.

Mit Hilfe der Totalreflexion von Licht oder Mikrowellen kann der Tunneleffekt veranschaulicht werden.